Hamming Code

 Hamming Code

Hamming code is a set of error-correction codes that can be used to detect and correct the errors that can occur when the data is moved or stored from the sender to the receiver. It is technique developed by R.W. Hamming for error correction.

Hamming code is a block code that is capable of detecting up to two simultaneous bit errors and correcting single-bit errors.

Error Correction codes are used to detect and correct the errors when data is transmitted from the sender to the receiver.

Error Correction can be handled in two ways:

• Backward error correction: Once the error is discovered, the receiver requests the sender to re transmit the entire data unit.
• Forward error correction: In this case, the receiver uses the error-correcting code which automatically corrects the errors.

In this coding method, the source encodes the message by inserting redundant bits within the message. These redundant bits are extra bits that are generated and inserted at specific positions in the message itself to enable error detection and correction. When the destination receives this message, it performs recalculations to detect errors and find the bit position that has error.

Redundant bits are extra binary bits that are generated and added to the information-carrying bits of data transfer to ensure that no bits were lost during the data transfer.

Encoding a message by Hamming Code

The procedure used by the sender to encode the message encompasses the following steps −

• Step 1 − Calculation of the number of redundant bits.
• Step 2 − Positioning the redundant bits.
• Step 3 − Calculating the values of each redundant bit.

Once the redundant bits are embedded within the message, this is sent to the user.

Step 1 − Calculation of the number of redundant bits.

The number of redundant bits can be calculated using the following formula:

 2^r ≥ m + r + 1

 where, r = redundant bit, m = data bit

Suppose the number of data bits is 7, then the number of redundant bits can be calculated using:
= 2^4 ≥ 7 + 4 + 1
Thus, the number of redundant bits= 4.

Step 2 − Positioning the redundant bits.

The r redundant bits placed at bit positions of powers of 2, i.e. 1, 2, 4, 8, 16 etc. They are referred as r₁ (at position 1), r₂ (at position 2), r₃ (at position 4), r₄ (at position 8) and so on.

Step 3 − Calculating the values of each redundant bit.

The redundant bits are parity bits. A parity bit is an extra bit that makes the number of 1s either even or odd. The two types of parity are −

• Even Parity − Here the total number of bits in the message is made even.
• Odd Parity − Here the total number of bits in the message is made odd.

Each redundant bit, r_i, is calculated as the parity, generally even parity, based upon its bit position.

Thus −

• r₁ is the parity bit for all data bits in positions whose binary representation includes a 1 in the least significant position excluding 1 (3, 5, 7, 9, 11 and so on)
• r₂ is the parity bit for all data bits in positions whose binary representation includes a 1 in the position 2 from right except 2 (3, 6, 7, 10, 11 and so on)
• r₃ is the parity bit for all data bits in positions whose binary representation includes a 1 in the position 3 from right except 4 (5-7, 12-15, 20-23 and so on)

Decoding a message in Hamming Code

Once the receiver gets an incoming message, it performs recalculations to detect errors and correct them. The steps for recalculation are −

• Step 1 − Calculation of the number of redundant bits.
• Step 2 − Positioning the redundant bits.
• Step 3 − Parity checking.
• Step 4 − Error detection and correction

Step 1 − Calculation of the number of redundant bits

Using the same formula as in encoding, the number of redundant bits is calculated.

2^r ≥ m + r + 1 where m is the number of data bits and r is the number of redundant bits.

Step 2 − Positioning the redundant bits

The r redundant bits placed at bit positions of powers of 2, i.e. 1, 2, 4, 8, 16 etc.

Step 3 − Parity checking

Parity bits are calculated based upon the data bits and the redundant bits using the same rule as during generation of c₁,c₂ ,c₃ ,c₄ etc. Thus

c₁ = parity (1, 3, 5, 7, 9, 11 and so on)

c₂ = parity (2, 3, 6, 7, 10, 11 and so on)

c₃ = parity (4-7, 12-15, 20-23 and so on)

Step 4 − Error detection and correction

The decimal equivalent of the parity bits binary values is calculated. If it is 0, there is no error. Otherwise, the decimal value gives the bit position which has error.

For example, if c₁c₂c₃c₄ = 1001, it implies that the data bit at position 9, decimal equivalent of 1001, has error. The bit is flipped to get the correct message.

Example:

Suppose the data to be transmitted is 1011001.

The number of data bits = 7

The number of redundant bits = 4. Using  2^r ≥ m + r + 1

The total number of bits = 11

The redundant bits are placed at positions corresponding to power of 2- 1, 2, 4, and 8

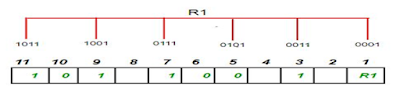
The data to be transmitted is 1011001, the bits will be placed as follows:

Determining the Parity bits –

1. R1 bit is calculated using parity check at all the bits positions whose binary representation includes a 1 in the least significant position.

R1: bits 1, 3, 5, 7, 9, 11

To find the redundant bit R1, we check for even parity. Since the total number of 1’s in all the bit positions corresponding to R1 is an even number the value of R1 (parity bit’s value) = 0.

2. R2 bit is calculated using parity check at all the bits positions whose binary representation includes a 1 in the second position from the least significant bit.

R2: bits 2,3,6,7,10,11

To find the redundant bit R2, check for even parity. Since the total number of 1’s in all the bit positions corresponding to R2 is odd the value of R2(parity bit’s value)=1

3. R4 bit is calculated using parity check at all the bits positions whose binary representation includes a 1 in the third position from the least significant bit.

R4: bits 4, 5, 6, 7`

To find the redundant bit R4, we check for even parity. Since the total number of 1’s in all the bit positions corresponding to R4 is odd the value of R4(parity bit’s value) = 1

4. R8 bit is calculated using parity check at all the bits positions whose binary representation includes a 1 in the fourth position from the least significant bit.

R8: bit 8,9,10,11

To find the redundant bit R8, we check for even parity. Since the total number of 1’s in all the bit positions corresponding to R8 is an even number the value of R8(parity bit’s value)=0.

Thus, the data transferred is:

Error detection and correction –
Suppose in the above example the 6th bit is changed from 0 to 1 during data transmission, then it gives new parity values in the binary number:

The bits give the binary number as 0110 whose decimal representation is 6. Thus, the bit 6 contains an error. To correct the error the 6th bit is changed from 1 to 0.

Advantages of Hamming code

• Hamming code method is effective on networks where the data streams are given for the single-bit errors.
• Hamming code not only provides the detection of a bit error but also helps you to indent bit containing error so that it can be corrected.
• The ease of use of hamming codes makes it best them suitable for use in computer memory and single-error correction.

Disadvantages of Hamming code

• Hamming code algorithm can solve only single bits issues.