Error Detection

Error detection techniques are responsible for checking whether any error has occurred or not in the frame that has been transmitted via network. It does not take into account the number of error bits and the type of error.

For error detection, the sender needs to send some additional bits along with the data bits. The receiver performs necessary checks based upon the additional redundant bits. If it finds that the data is free from errors, it removes the redundant bits before passing the message to the upper layers.

The most popular Error Detecting Techniques are:

• Single parity check (Vertical Redundancy Check)
• Two-dimensional parity check (Longitudinal Redundancy Check)
• Checksum
• Cyclic redundancy check

 Single Parity Check

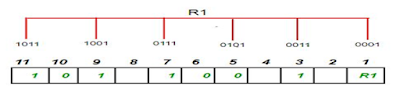
 Single Parity checking is the simple mechanism and inexpensive to detect the errors. In this technique, a redundant bit is also known as a parity bit which is appended at the end of the data unit so that the number of 1s becomes even. Therefore, the total number of transmitted bits would be 9 bits.

 If the number of 1s bits is odd, then parity bit 1 is appended and if the number of 1s bits is even, then parity bit 0 is appended at the end of the data unit. At the receiving end, the parity bit is calculated from the received data bits and compared with the received parity bit. This technique generates the total number of 1s even, so it is known as even-parity checking.

Drawbacks of Single Parity Checking

• It can only detect single-bit errors which are very rare.
• If two bits are interchanged, then it cannot detect the errors.

Two-Dimensional Parity Check

Performance can be improved by using Two-Dimensional Parity Check which organizes the data in the form of a table.

Parity check bits are computed for each row, which is equivalent to the single-parity check.

In Two-Dimensional Parity check, a block of bits is divided into rows, and the redundant row of bits is added to the whole block.

At the receiving end, the parity bits are compared with the parity bits computed from the received data.

Drawbacks of 2D Parity Check

 If two bits in one data unit are corrupted and two bits exactly the same position in another data unit is also corrupted, then 2D Parity checker will not be able to detect the error.

Checksums

 This is a block code method where a checksum is created based on the data values in the data blocks to be transmitted using some algorithm and appended to the data. When the receiver gets this data, a new checksum is calculated and compared with the existing checksum. A non-match indicates an error.

 Error Detection by Checksums

For error detection by checksums, data is divided into fixed sized frames or segments.

 

• Sender’s End − The sender adds the segments using 1’s complement arithmetic to get the sum. It then complements the sum to get the checksum and sends it along with the data frames.
• Receiver’s End − The receiver adds the incoming segments along with the checksum using 1’s complement arithmetic to get the sum and then complements it.

If the result is zero, the received frames are accepted; otherwise they are discarded.

 Suppose that the sender wants to send 4 frames each of 8 bits, where the frames are 11001100, 10101010, 11110000 and 11000011.

 The sender adds the bits using 1s complement arithmetic. While adding two numbers using 1s complement arithmetic, if there is a carry over, it is added to the sum.

After adding all the 4 frames, the sender complements the sum to get the checksum, 11010011, and sends it along with the data frames.

The receiver performs 1s complement arithmetic sum of all the frames including the checksum. 

The result is complemented and found to be 0. Hence, the receiver assumes that no error has occurred.

Cyclic Redundancy Check (CRC)

Cyclic Redundancy Check (CRC) is a block code invented by W. Wesley Peterson in 1961.

CRC involves binary division of the data bits being sent by a predetermined divisor agreed upon by the communicating system. The divisor is generated using polynomials. So, CRC is also called polynomial code checksum.

Given a k-bit frame or message, the transmitter generates an n-bit sequence, known as a frame check sequence (FCS), so that the resulting frame, consisting of (k+n) bits, is exactly divisible by some predetermined number.

Encoding using CRC

The communicating parties agree upon the size of message block and the CRC divisor. The sender performs binary division of the data segment by the divisor.

Sender then appends the remainder called CRC bits to the end of data segment. This makes the resulting data unit exactly divisible by the divisor.

Decoding

The receiver divides the incoming data unit by the divisor. If there is no remainder, the data unit is assumed to be correct and is accepted.

Otherwise, it is understood that the data is corrupted and is therefore rejected. The receiver may then send an erroneous acknowledgement back to the sender for retransmission.

Suppose the original data is 11100 and divisor is 1001.

CRC Generator

A CRC generator uses a modulo-2 division. Firstly, three zeroes are appended at the end of the data as the length of the divisor is 4 and we know that the length of the string 0s to be appended is always one less than the length of the divisor.

Now, the string becomes 11100000, and the resultant string is divided by the divisor 1001.

The remainder generated from the binary division is known as CRC remainder. The generated value of the CRC remainder is 111. CRC remainder replaces the appended string of 0s at the end of the data unit, and the final string would be 11100111 which is sent across the network.

CRC Checker

The functionality of the CRC checker is similar to the CRC generator.

When the string 11100111 is received at the receiving end, then CRC checker performs the modulo-2 division. A string is divided by the same divisor, i.e., 1001.

In this case, CRC checker generates the remainder of zero. Therefore, the data is accepted.

 

Hamming Code

 Hamming Code

Hamming code is a set of error-correction codes that can be used to detect and correct the errors that can occur when the data is moved or stored from the sender to the receiver. It is technique developed by R.W. Hamming for error correction.

Hamming code is a block code that is capable of detecting up to two simultaneous bit errors and correcting single-bit errors.

Error Correction codes are used to detect and correct the errors when data is transmitted from the sender to the receiver.

Error Correction can be handled in two ways:

• Backward error correction: Once the error is discovered, the receiver requests the sender to re transmit the entire data unit.
• Forward error correction: In this case, the receiver uses the error-correcting code which automatically corrects the errors.

In this coding method, the source encodes the message by inserting redundant bits within the message. These redundant bits are extra bits that are generated and inserted at specific positions in the message itself to enable error detection and correction. When the destination receives this message, it performs recalculations to detect errors and find the bit position that has error.

Redundant bits are extra binary bits that are generated and added to the information-carrying bits of data transfer to ensure that no bits were lost during the data transfer.

Encoding a message by Hamming Code

The procedure used by the sender to encode the message encompasses the following steps −

• Step 1 − Calculation of the number of redundant bits.
• Step 2 − Positioning the redundant bits.
• Step 3 − Calculating the values of each redundant bit.

Once the redundant bits are embedded within the message, this is sent to the user.

Step 1 − Calculation of the number of redundant bits.

The number of redundant bits can be calculated using the following formula:

 2^r ≥ m + r + 1

 where, r = redundant bit, m = data bit

Suppose the number of data bits is 7, then the number of redundant bits can be calculated using:
= 2^4 ≥ 7 + 4 + 1
Thus, the number of redundant bits= 4.

Step 2 − Positioning the redundant bits.

The r redundant bits placed at bit positions of powers of 2, i.e. 1, 2, 4, 8, 16 etc. They are referred as r₁ (at position 1), r₂ (at position 2), r₃ (at position 4), r₄ (at position 8) and so on.

Step 3 − Calculating the values of each redundant bit.

The redundant bits are parity bits. A parity bit is an extra bit that makes the number of 1s either even or odd. The two types of parity are −

• Even Parity − Here the total number of bits in the message is made even.
• Odd Parity − Here the total number of bits in the message is made odd.

Each redundant bit, r_i, is calculated as the parity, generally even parity, based upon its bit position.

Thus −

• r₁ is the parity bit for all data bits in positions whose binary representation includes a 1 in the least significant position excluding 1 (3, 5, 7, 9, 11 and so on)
• r₂ is the parity bit for all data bits in positions whose binary representation includes a 1 in the position 2 from right except 2 (3, 6, 7, 10, 11 and so on)
• r₃ is the parity bit for all data bits in positions whose binary representation includes a 1 in the position 3 from right except 4 (5-7, 12-15, 20-23 and so on)

Decoding a message in Hamming Code

Once the receiver gets an incoming message, it performs recalculations to detect errors and correct them. The steps for recalculation are −

• Step 1 − Calculation of the number of redundant bits.
• Step 2 − Positioning the redundant bits.
• Step 3 − Parity checking.
• Step 4 − Error detection and correction

Step 1 − Calculation of the number of redundant bits

Using the same formula as in encoding, the number of redundant bits is calculated.

2^r ≥ m + r + 1 where m is the number of data bits and r is the number of redundant bits.

Step 2 − Positioning the redundant bits

The r redundant bits placed at bit positions of powers of 2, i.e. 1, 2, 4, 8, 16 etc.

Step 3 − Parity checking

Parity bits are calculated based upon the data bits and the redundant bits using the same rule as during generation of c₁,c₂ ,c₃ ,c₄ etc. Thus

c₁ = parity (1, 3, 5, 7, 9, 11 and so on)

c₂ = parity (2, 3, 6, 7, 10, 11 and so on)

c₃ = parity (4-7, 12-15, 20-23 and so on)

Step 4 − Error detection and correction

The decimal equivalent of the parity bits binary values is calculated. If it is 0, there is no error. Otherwise, the decimal value gives the bit position which has error.

For example, if c₁c₂c₃c₄ = 1001, it implies that the data bit at position 9, decimal equivalent of 1001, has error. The bit is flipped to get the correct message.

Example:

Suppose the data to be transmitted is 1011001.

The number of data bits = 7

The number of redundant bits = 4. Using  2^r ≥ m + r + 1

The total number of bits = 11

The redundant bits are placed at positions corresponding to power of 2- 1, 2, 4, and 8

The data to be transmitted is 1011001, the bits will be placed as follows:

Determining the Parity bits –

1. R1 bit is calculated using parity check at all the bits positions whose binary representation includes a 1 in the least significant position.

R1: bits 1, 3, 5, 7, 9, 11

To find the redundant bit R1, we check for even parity. Since the total number of 1’s in all the bit positions corresponding to R1 is an even number the value of R1 (parity bit’s value) = 0.

2. R2 bit is calculated using parity check at all the bits positions whose binary representation includes a 1 in the second position from the least significant bit.

R2: bits 2,3,6,7,10,11

To find the redundant bit R2, check for even parity. Since the total number of 1’s in all the bit positions corresponding to R2 is odd the value of R2(parity bit’s value)=1

3. R4 bit is calculated using parity check at all the bits positions whose binary representation includes a 1 in the third position from the least significant bit.

R4: bits 4, 5, 6, 7`

To find the redundant bit R4, we check for even parity. Since the total number of 1’s in all the bit positions corresponding to R4 is odd the value of R4(parity bit’s value) = 1

4. R8 bit is calculated using parity check at all the bits positions whose binary representation includes a 1 in the fourth position from the least significant bit.

R8: bit 8,9,10,11

To find the redundant bit R8, we check for even parity. Since the total number of 1’s in all the bit positions corresponding to R8 is an even number the value of R8(parity bit’s value)=0.

Thus, the data transferred is:

Error detection and correction –
Suppose in the above example the 6th bit is changed from 0 to 1 during data transmission, then it gives new parity values in the binary number:

The bits give the binary number as 0110 whose decimal representation is 6. Thus, the bit 6 contains an error. To correct the error the 6th bit is changed from 1 to 0.

Advantages of Hamming code

• Hamming code method is effective on networks where the data streams are given for the single-bit errors.
• Hamming code not only provides the detection of a bit error but also helps you to indent bit containing error so that it can be corrected.
• The ease of use of hamming codes makes it best them suitable for use in computer memory and single-error correction.

Disadvantages of Hamming code

• Hamming code algorithm can solve only single bits issues.